Vigésimo cuarta sesión: Discretización de señales.

Hemos empezado la clase repasando el temario de respuesta completa de circuitos, cosa que personalmente he agradecido, así he acabado de concretar las ideas abstractas que tenía en mente después de leerme las notas de clase, y hemos añadido un criterio para descartar bastantes circuitos de ser inestables.

Una vez finalizada esta explicación, hemos empezado a hablar sobre como analizar señales arbitrarias, sin forma ni norma. El truco está en aproximar la función usando la derivada de la tensión y la tensión en el último estado, parece un problema simple, pero en realidad se necesitan procesadores bastante potentes para realizar esos cálculos que resultan ser bastante complejos.

Y hasta aquí ha durado el temario de las clases de Circuitos Lineales, una asignatura que a mi entender me ha aportado mucho conocimiento sobre cosas que ni tan siquiera imaginaba. Durante el curso hemos comprendido y descubierto filtros paso-bajos, paso-banda, paso-altos, lineas de transmisión, AOs, y a transformar cualquier señal periódica en una suma de senoides, y sobretodo, hemos aprendido a generar tensiones senoidales a frecuencias fijas, cosa que al principio de quatrimestre no teníamos ni idea de como hacer.

Nos vemos, y sed buenos.

J.

Vigésimo tercera sesión: Respuesta completa de un circuito

Vigésimo segunda sesión: Transformada de Laplace

Vigésimo primera sesión: Diseño frecuencial.

Lamentablemente no pude asistir a esta sesión, ni podré asistir a las dos siguientes, así que no puedo publicar mis resúmenes, lo siento.

Vigésima sesión: La intervención inesperada de Fourier.

Hoy hemos dejado de lado el tema de Bode para centrarnos en algo infinitamente más interesante, las alimentaciones arbitrarias. Nos hemos basado en la teoría de las series de Fourier (matemático francés de los siglos XVIII y XIX), para postular que toda excitación periódica podía ser descompuesta en una suma convergente de senoides de frecuencias fo y n*fo (donde n pertentece a los naturales).

Una vez explicada la teoría nos hemos centrado en la representación de esta, ¿como mostrar las senoides de que consta una entrada? Pues para eso nos servimos de los espectrales, que son unos gráficos en cuyo eje de abscisas se encuentran las frecuencias propias de la entrada y en el otro se encuentra el módulo de esas frecuencias en dBmicroV.

Hemos analizado también la precisión de este análisis, comprobando que cogiendo solo 3 términos de la serie obteníamos una precisión de 90%, lo cual no está nada mal.

Décimo novena sesión: Los picos de resonancia contraatacan

Hoy hemos continuado el tema de nuestro polinomio de segundo grado, esclareciendo más propiedades de esta y sacando a la luz sus secretos. Hemos hallado el ancho de banda de esta función, observando que para ρ menor que 0.1, este ancho de banda se convierte en 2*ρ*ω  y hemos definido también el factor de calidad del pico de resonancia, un número que nos indica el valor de su anchura máxima en función de su frecuencia. Y hemos procedido a realizar unos cuantos ejercicios para acabar de asentar el tema.

En la segunda parte de la clase hemos debatido sobre las aplicaciones de estos picos, por ejemplo en radiorreceptores  y parecidos, y sobre como trabajar en PSPICE y hacer análisis de la funciones de Bode.

Décimo octava sesión: La resonancia

Hoy nos hemos dedicado otra vez a realizar trazados de bode de diferentes circuitos, ampliando los conocimientos adquiridos en la anterior clase, hasta que nos hemos encontrado con un problema con una H(s) con un polinomio de segundo grado en el denominador. Hemos definido entonces, una nueva forma de tratar los polinomios de segundo grado dejando sus constantes en función de ρ y ω, simplificando el cálculo de su trazado de Bode.

Pero la verdadera sorpresa apareció cuando analizamos el trazado real y observamos que en la frecuencia de corte la ganancia era positiva, produciéndose un pico de potencia de salida. Y hemos parametrizado ese pico en función de ρ detectando para que valores se produce ganancia y para cuales pérdida.

Décimo séptima sesión: Hendrik Wade Bode

Hoy hemos vuelto a nuestra querida función de red para encontrar algún método eficaz para representarla en el domino de las frecuencias, a modo de poder hacer predicciones de su comportamiento ante estas. La solución que se nos ha planteado en clase es usar el método de los trazados de Bode.

Los trazados de bode, se basan en subdividir la H(s) de nuestro circuito en productos de polinomios de grado 1 y sumar las representaciones de Bode de estas. La representación de Bode de un polinomio simple se hace hallando lo que llamaremos frecuencia de corte del circuito, que es el punto donde el módulo de la H(s) vale 0.707, y representando graficamente el valor que sale cuando f tiende a 0 por el lado inferior y cuando f tiende a infinito por el lado superior, en un gráfico graduado logaritmícamente.

Hemos analizado los trazados de Bode de varias H(s), y comprobado las perdidas que había en el análisis al representar los trazados de Bode, que hemos visto que era mínimas.

Décimo sexta sesión: El fin del Transformador Perfecto y el Teorema de la Máxima Potencia

Hoy hemos dedicado la clase a buscar y encontrar métodos para conseguir que pudiésemos aproximar el transformador perfecto por uno de ideal. Después de estudiar cada uno de ellos, creo que podríamos hacer esta clasificación:

• Casos en que la frecuencia de trabajo es muy alta: Debido a la naturaleza del comportamiento del inductor a altar frecuencias, este se puede aproximar por un circuito abierto, dejando solo el transformador ideal.
• Transformadores con inductancia de entrada muy alta: Porque en ellos se dará el caso anterior a frecuencias inferiores.
• Casos en los que la frecuencia es fija: En estos casos, podemos conectar un condensador en paralelo con el inductor de capacidad tal que ambos entren en resonancia a dicha frecuencia, convirtiendo la impedancia equivalente del bipolo en un circuito abierto.

Además, también hemos anunciado el Teorema de la Máxima Potencia, que nos cuenta de forma efectiva como extraer la máxima potencia posible de un generador. Esto se hace conectándolo a un circuito cuya impedancia equivalente sea idéntica a su impedancia interna, cosa que podemos hacer en cualquier circuito gracias a nuestro nuevo amigo, el Transformador.

 

Décimo quinta sesión: El transformador perfecto y sus secretos.

Hemos iniciado la clase recordando el componente etéreo que habíamos introducido en la anterior sesión, el transformador ideal, y realizando varios ejercicios para poner en relieve su comportamiento descrito en la anterior sesión. Justo después pasamos al meollo de la cuestión, como construir físicamente transformadores.

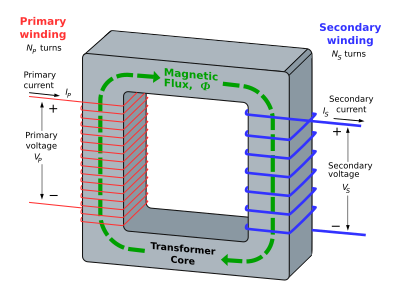
Ante eso, nuestro profesor automáticamente nos presentó el diseño de un aparato formado por dos bobinas de material conductor devanadas sobre un núcleo de ferrita, y con la ayuda de las leyes de Faraday-Lenz, descubrimos apasionados que en su modelo circuital aparecía un transformador ideal, en paralelo con una inductancia. Nos parece una buena aproximación, tiene la desventaja de que no funcionará en corriente continua y que la impedancia del inductor influirá en el circuito, pero es la mejor aproximación. Hemos llamado a este dispositivo "Transformador Perfecto".

Décimo cuarta sesión: Los transformadores y sus tratos con el diablo.

Hemos empezado la sesión con unos cuantos ejemplos de lo explicado el día anterior sobre líneas de transmisión, aclarando muchos cabos sueltos que quedaban por atar, y permitiéndonos verlo todo con un poco más de perspectiva, ya que el último día acabamos apabullados con tanto dato.

Entonces no hemos puesto a pensar, y nos hemos planteado, ¿y si la impedancia equivalente de nuestro circuito no encaja con ninguno de los modelos de cable coaxial que hay en el mercado? ¿deberíamos hacer un cable especial para cada circuito? A lo que el profesor nos ha contestado que no, que lo que necesitábamos era modificar la resistencia equivalente añadiendo un nuevo elemento: el transformador.

Tratando en el mundo etéreo de los elementos ideales, hemos diseñado un dispositivo cuya tensión de entrada e intensidad de entrada eran proporcionales a sus homónimas en la salida respecto a una constante n. Hemos observado como se comportaba con las resistencias, y hemos visto que a efectos prácticos, desde los terminales de entrada estas se veían modificadas! Y lo mismo con los condensadores e inductores!

Vamos a tener que estudiar mejor que especie de tratos con el diablo se lleva este componente y como podríamos crearlo en la vida real.

Décimo tercera sesión: La magia oculta de las lineas de transmisión.

Después de un brevissimo resumen de la sesión anterior, nos hemos centrado en otro problema bastante importante, ¿como podríamos transportar información a través de distancias enormes? Bien, ante ese problema, nuestro profesor nos ha dicho: "no se trata de trasportar la energía al circuito de salida, sino de transportar el circuito de salida al lado de la entrada" indicando que lo que deberíamos hacer es conseguir que la entrada de la transmisión tenga la misma impedancia equivalente que el circuito que queramos conectar.

Entonces nos ha introducido un circuito formado por un inductor, un condensador y una resistencia que tenía la maravillosa propiedad de tener una impedancia equivalente del mismo valor que la resistencia, y nos ha preguntado que pasaría si pusiéramos muchos circuitos como ese conectados en escala. De ahí ha surgido el diseño de el cable coaxial, basado en simular esa estructura, y hemos pasado el resto de la clase estudiando su comportamiento y sus pérdidas.

La clase ha sido realmente densa y cargada, pero vale la pena escucharla, se ha aprendido muchas cosas útiles.

Duodécima sesión: La potencia contraataca

Hoy hemos dedicado nuestra apasionante clase a realizar ejercicios de cálculo de potencia, a modo de ampliar las definiciones vistas en la anterior sesión. Después de analizar varios circuitos, hemos establecido varios tipos de análisis en función de la alimentación:

• Senoidales a la misma frecuencia: No se aplica superposición, se calcula el módulo de la tensión en el nodo y Vrms.
• Senoidales a distinta frecuencia: Aplicamos superposición.
• Tensiones arbitrarias: Hallamos Vrms del elemento en cuestión.

Después de un cálculo elaborado, llegamos a la conclusión de que los únicos elementos que disipaban potencia en el circuito eran los resistores.

Y antes de acabar de clase hemos introducido un tema realmente interesante, los decibelios! El profesor nos ha contado que los definió Alexander Graham Bell para realizar cálculos para sus líneas telefónicas, y nos ha mostrado varias de sus propiedades, que realmente parecen mágicas. Con decibelios podemos determinar la potencia de salida de un circuito simplemente realizando una suma!

Undécima entrada: Potencia.

Hoy hemos empezado a contar el tema de potencia, que parece que va a tener miga y darnos bastante trabajo. Hemos empezado definiendo el concepto potencia, y nos hemos percatado de que necesitábamos más descriptores para simplificar los cálculos, así, hemos definido:

• Tensión media: es la tensión constante que surge de calcular la integral definida de la tensión de entrada a lo largo de un periodo, y dividirla por el periodo. Aporta mucha información del circuito, pero nos percatamos de que cuando la entrada es, por ejemplo, una tensión senoidal, esta tensión tiene un valor nulo, y en cambio, podemos apreciar que la potencia disipada no lo es, lo cual nos lleva al siguiente descriptor.
• Tensión RMS (Root Medium Square): es la tensión constante que surge de hacer la raíz cuadrada de la tensión media del cuadrado de la tensión original. Tiene la ventaja respecto la tensión media, de que nos da un resultado válido para tensiones simétricas, permitiéndonos analizar senoides.

El resto de la clase hemos aplicado estos descriptores a las fórmulas de potencia, y hemos analizado un par de circuitos, adquiriendo un poco de perspectiva sobre la potencia.

Décima entrada: Últimos toques al AO

En esta sesión nos hemos dedicado a profundizar un poco más sobre las aplicaciones de un AO trabajando en modo de comparación, y hemos definido el parámetro "ciclo de trabajo", que indica el porcentaje de ciclo en que el AO tiene en la salida la alimentación positiva.

Además, hemos estudiado un par de circuitos con el AO donde este se comportaba como puerta NAND, temporizador... Increible.

Además, hemos estado analizando el comportamiento del AO si en vez de conectar la realimentación al nodo negativo, lo hiciéramos con el positivo, y hemos visto que se volvía inestable, tendiendo a huir de la zona lineal, de forma que hemos decidido no trabajar con él de esta forma.

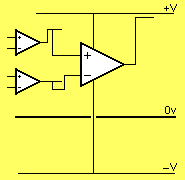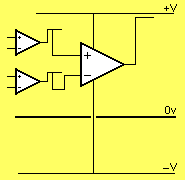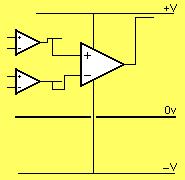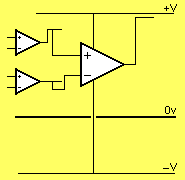
Y al final hemos dedicado el resto de la clase a resolver la duda de un compañero, que sucedería si el AO no tuviera a alimentación simétrica.

Novena sesión: Diseño modular.

Al inicio de la clase hemos hecho un breve repaso de los AOs, cosa que después de las vacaciones se agradece bastante, pero el resto de la clase lo hemos dedicado al estudio y diseño de los llamados "Bloques Operacionales".

Un bloque operacional es un circuito que realiza una operación concreta parametrizable cuya salida se comporta como una fuente ideal de tensión. Hemos creado un pequeño Set de bloques, con cuyas operaciones y conociendo la H(s) del circuito, hemos aprendido a diseñar circuitos.

Los bloques que hemos creado son:

• Miltiplicador xC (C > 1)
• Miltiplicador xC (C < 1)
• Inversor (Cambia el signo de la entrada)
• Restador
• Integrador

Y para terminar la sesión, hemos visto una de las posiblidades del AO cuando no está realimentado, el uso del AO como comparador de tensiones.

Octava sesión: Usos del AO.

En la última sesión presentamos el AO y dos de sus circuitos más básicos, el amplificador no inversor, y su contrario, el amplificador inversor, dos circuitos que nos serán verdaderamente útiles cuando trabajemos con ellos, y hoy nos hemos dedicado a analizar más circuitos posibles con AOs.

Así, hemos hallado un circuito que nos permitía restar tensiones, y después de analizar el comportamiento de los AOs cuando son conectados en cascada, hemos hallado circuitos capaces de sumar, restar, multiplicar por una constante, e incluso integrar y derivar tensiones!

Además hemos comprobado que la salida de un AO se comporta como una fuente ideal de tensión, y que utilizando seguidores de tensión (multiplicadores x1) conseguimos crear circuitos cuya impedancia de entrada es infinita, que cuando se conectan a un circuito no alteran su comportamiento.

Ante estos resultados, se nos enciende un diodo LED, y comprendemos la denominación de "operacional" de este circuito.

(No encontré imágenes de ningún diodo LED)

Séptima sesión: AOs

En la anterior sesión se nos presentó un generador senoidal que emitia una senoide de frecuencia 1/(2*Pi*RC), el circuito era de diseño sencillo, pero nos encontramos con una dificultad: no sabemos como crear una fuente dependiente.

Y como solución a este problema, se nos aparece, como caído del cielo, un dispositivo llamado Amplificador Operacional (AO, de ahora en adelante), que es un dispositivo cuya salida es la amplificación de la diferencia de potencial entre dos de sus entradas multiplicada por un factor de amplificación enorme y acotada por un voltaje un poco inferior a su tensión de alimentación.

Parece un dispositivo no-lineal, pero hemos descubierto las maravillas de la retroalimentación, es decir, hacer que Vo influya en la tensión de la entrada marcada como negativa, este sorprendente dispositivo se convierte en lineal, PERMITIÉNDONOS HACER INFINIDAD DE COSAS ÚTILES.

Datasheet de un AO de Texas Instruments

Sexta sesión: "El Método".

En esta clase hemos presentado lo que llamamos: Análisis metódico de circuitos. Este es un procedimiento que nos permite analizar todo tipo de circuitos lineales independientemente de su forma o estructura.


El Método:

• Hipótesis de partida:

Partimos de la hipótesis de que las tensiones nodales son variables generadoras, es decir, que a partir de ella podemos obtener cualquier dato del circuito.

• Estrategia:

Dada esa hipótesis inicial, nuestro objetivo será detectar los valores de las tensiones de N-1 nodos respecto al nodo resultante, que llamaremos "nodo de referencia" y cuya tensión consideraremos nula.

• Procedimiento:

Para obtener esas N-1 tensiones, planteamos los KCLs de cada uno de los N-1 nodos y resolvemos esas ecuaciones.

• Modificación:

¿Que sucede cuando tenemos un generador de tensión conectado entre un nodo y el de referencia? Esto puede parecer un problema, ya que no podemos determinar la intensidad que fluye por esa rama del circuito, pero en realidad es todo lo contrario, al tener ese generador conectado entre el nodo y el de referencia, ya sabemos que tensión tiene ese nodo, reduciendo nuestras N-1 incógnitas a N-2 incógnitas.


_______________________________________________________________

Al final de la clase, hemos resuelto varios ejercicios entre los cuales se encontraba uno que consistía en hallar la función de red del siguiente circuito:

Donde nos encontrábamos que su H(s) para K = 3, tenía cierta frecuencia en que la H(s) pasaba a valer infinito, y el profesor nos ha contado que eso significa que, sin el generador senoidal, el circuito generará una senoide de frecuencia f = 1/(2πRC). Ya hemos hallado pues, un diseño de generador senoidal, ahora solo nos falta averiguar cómo diseñar una fuente dependiente de tensión, cosa que averiguaremos en la próxima entrada.

Quinta sesión: Admitancia, conductancia, susceptancia.

En la anterior clase mencionamos el concepto de Impedancia, bien, pues en la sessión de hoy hemos analizado mejor este concepto, descomponiendola en 2 componentes:

• Resistencia: Que es la parte real de la impedancia.
• Reactancia: Que es la parte imaginaria de la impedancia.

Además, hemos introducido el concepto de admitancia (Y), que es el inverso de la impedancia  un concepto muy potente porque sus operaciones de combinación de admitancias están intercambiadas respecto las de la impedancia. Además, también la podemos descomponer en dos componentes:

• Conductancia: Parte real de la admitancia.
• Susceptancia: Parte imaginaria de la admintancia.

Y hemos aprendido que a partir de la impedancia o admitancia de un bipolo, podemos proponer otros bipolos cuya impedancia sea la misma y que por lo tanto sean equivalentes en el momento de diseñar un circuito.

Además, hemos hecho ademán en la posibilidad de cometer errores en el cálculo de la H(jω) debido a los números complejos, y hemos decidido simplificar el cálculo con el cambio de variable:

 s = jω

Cuarta sesión: Classe práctica.

En esta sesión, después de muchos días contando teoría y sin probarla, por fin hemos puesto en práctica todo lo aprendido anteriormente.

Al inicio de la clase hemos introducido el concepto impedancia, que es una resistencia compleja y también hemos explicado la relación entre el fasor tensión y el fasor instensidad.

Posteriormente hemos empezado a resolver circuitos relacionados con los últimos temarios explicados en la asignatura. Aprovechando esta resolución hemos visto métodos bastante prácticos para la resolución de circuitos, como son el uso dela ecuacion del divisor de tensión, las combinaciones de resisténcias y superposición.

En el último ejercicio hemos introducido el concepto de función de red, que consiste en una función dependiente de la frecuencia, que nos indica la relación entre la entrada y la salida del circuito para una frecuencia específica de alimentación.

    H(jω) = Vo/Vg

Tercera sesión: Sinusoides y fasores, el Circuito transformado fasorial.

Qué es una senoide?

Una senoide es una función periódica que corresponde a la forma de una función trigonométrica seno o coseno con una determinada pulsación y un determinado desfase. Es decir, una senoide es una función del tipo:

v(t) = Vm * cos (w*t - ß);  Vm,w € R ;  -2Pi <=  ß <= 2Pi;

Donde:

• Vm => Amplitud de la senoide.
• w => Pulsación en rad/s o w = 2Pi*f.
• ß => Angulo de desfase en radianes.

También se puede expresar como que:

v(t) = Re[Vm * e^(jß) * e^j(wt)]

Fasor asociado a una senoide

Si tenemos una senoide de pulsación w, de la forma:

v(t) = Re[z]; → Donde z = Vm * e^(jß) * e^j(wt); z € C

Definimos el fasor asociado a una senoide como el complejo resultante de dividirlo entre e^j(wt).

       v(t) = z/e^j(wt) = Vm * e^(jß)

Este concepto nos permite simplificar cálculos al pasar las funciones del circuito al dominio fasorial, por ejemplo:

v4(t) = v1(t) + v2(t) + v3(t)
↓

V4m*cos(wt - ß4) = V1m*cos(wt - ß1) + V2m*cos(wt - ß2) + V3m*cos(wt - ß3)
↓
Re[V4m * e^(jß4) * e^j(wt)] = Re[V1m * e^(jß1) * e^j(wt) + V2m * e^(jß2) * e^j(wt) + V3m * e^(jß3) * e^j(wt))]
↓
V4m * e^(jß4) * e^j(wt) = V1m * e^(jß1) * e^j(wt) + V2m * e^(jß2) * e^j(wt) + V3m * e^(jß3) * e^j(wt))
↓
[V4m * e^(jß4)] * e^j(wt) = [V1m * e^(jß1)  + V2m * e^(jß2) + V3m * e^(jß3)] * e^j(wt)
↓
V4m * e^(jß4) = V1m * e^(jß1)  + V2m * e^(jß2) + V3m * e^(jß3)
↓
[  v4 = v1 + v2 + v3  ]

Segunda sesión: Modelo circuital, elementos circuitales y del circuito al sistema de ecuaciones.

Modelo Circuital:

Es una presentación conceptual de los fenómenos físicos más relevantes que tienen lugar en el circuito, a partir de él se puede deducir un sistema de ecuaciones que pueda servirnos para conocer y predecir su funcionamiento. 

Lo principales fenómenos que hallaremos serán:

• Disipación de energía.
• Almacenamiento de energía:
• En forma de campo magnético.
• En forma de campo eléctrico.
• Generación :
• de tensiones.
• de corriente.

El modelo circuital nos puede ser útil para ver la estructura del circuito, para representar los elementos usaremos el elemento de circuito:

Elementos lineales:

Tenemos aquí un listado de los distintos elementos lineales que debemos conocer para esta asignatura con su correspondiente relacion v = f(i):

• Resistor:

V = R*I // P = V*I

• Condensador:

I = C(dV/dt) // P = V*C*(dV/dt)

• Autoinductancia:

V = L*(dI/dt) // P = I*L*(dI/dt)

• Fuente ideal de tensión:

• Fuente ideal de corriente:

• Fuentes dependientes de tensión y corriente:

Del circuito físico al modelo circuital:

Para dar este paso, tenemos que observar la estructura de nuestro circuito y considerar los fenómenos físicos más relevantes que en él suceden. No podemos tomarlos todos, ya que eso aumentaría exponencialmente la dificultad de resolución del circuito, ni tampoco podemos pasar por alto fenómenos relevantes, ya que eso convertiría el estudio en inexacto. El paso de circuito físico a modelo circuital es un arte, únicamente aprendido por la experiencia, en el que se debe tener habilidad.

Del modelo al sistema de ecuaciones:

Este es el último paso para pasar de circuito físico a las ecuaciones que describan su comportamiento. Se basa en anotar todas las relaciones v = f(i) de los elementos que hallemos en el circuito y combinarlas con las leyes de Kirchoff, a modo de obtener un sistema de ecuaciones compatible determinado a partir del cual podamos determinar el funcionamiento del circuito.

Observamos que en ocasiones, habitualmente cuando hay condensadores o autoinductancias en el circuito, nos aparece un sistema de ecuaciones con ecuaciones no lineales, esos sistemas son complejos de resolver, de hecho aún están en estudio, así que más adelante explicaremos algún método para convertirlos en sistemas de ecuaciones lineales.

Fin de la segunda sesión, de vuelta el viernes.

J

Introducción + Primeras lecciones

Hoy la clase ha consistido en la introducción por parte del profesor de la asignatura de Circuitos Lineales, perteneciente al segundo cuatrimestre del primer curso del grado en Ciencias y Tecnologías de Telecomunicación en la Universitat Politècnica de Catalunya. Uno de los puntos tratados sobre la asignatura ha sido el hecho de que cada alumno debe iniciar su propio blog comentando a diario las distintas sesiones de clase del curso, para realizar así un resumen del temario y asegurar que se ha comprendido lo explicado durante la hora lectiva, pues "no puedes estar seguro de que sabes una cosa hasta que no eres capaz de explicársela a alguien que no la haya escuchado nunca". Bien, este es mi blog y esta viene a ser la publicación de abertura. Con eso finaliza la parte de introducción que concierne a este blog, prosigamos con el temario explicado.

Para poder cursar una asignatura hay que saber que temario se va a dar en ella. Bien, esta asignatura trata sobre circuitos, pero ¿que es un circuito?.

"Un circuito es un conjunto de elementos que permiten el paso de corriente eléctrica a través suyo conectados de forma que exista al menos un camino cerrado." 

Bien, eso acota un poco nuestro rango de objetos de estudio, pero ¿para que sirve un circuito? Bien, un circuito nos puede ser útil des de dos puntos de vista:

• Procesar información.
• Procesar energía.

En esta asignatura no nos centraremos en el proceso de energía, pues esto es algo que no pertenece al rango de intereses del grado, lo que realmente nos interesa profundizar es en el estudio del circuito como elemento procesador de información.

Aún así, existen infinitos tipos de circuitos y no podemos abarcarlos todos, abarcaremos pues un pequeño rango de ellos, los circuitos de tamaño reducido. Elegimos estos circuitos porque debido a su tamaño se reducen en gran manera los fenómenos externos que podrían afectar a su funcionamiento, llegando a ser despreciables. Es en esos circuitos donde podemos aplicar leyes como las de Kirchoff o Ohm.

Pero, ¿que tipo de fenómenos pueden afectar nuestro circuito con el tamaño? Bueno, un ejemplo de ellos sería la velocidad de movimiento de los electrones, que es limitada, y podría provocar un desfase en la reacción de los distintos elementos a un impulso. El tiempo que tarda un electrón en viajar des del generador de tensión hasta un elemento del circuito viene definido por la siguiente fórmula:

t = l/c

Donde l es la distancia física del generador al elemento y c la velocidad de la luz.
Para considerar este fenómeno despreciable al aplicar una onda como alimentación del circuito, estableceremos que el tiempo que tarden los electrones a desplazarse hasta el elemento más lejano del circuito debe ser menor al 1% del periodo de esa onda. Al aplicar los cambios pertinentes y aislar la longitud nos queda la siguiente fórmula, que determina la distancia máxima que puede haber entre dos elementos de un circuito a determinada frecuencia:

l < 0'01*(f/c)

Una vez dada esa fórmula, podemos establecer una tabla de distancias máximas entre elementos en función de la frecuencia a la que se vean sometidos:

1 KHz  =>  3 km

1 MHz => 3 m

 27 MHz => 11 cm

1 GHz => 3 mm

De esa forma podemos discernir entre circuitos grandes y circuitos pequeños en función de la frecuencia de alimentación del circuito.

Y aquí acabó la clase, esa fue toda la lección, continuaré el martes, con la siguiente clase teórica.

J